TFA in der Forschung
Wenn DFT, Wavelet und Wigner nicht weiterhelfen:
Zur Berechnung von Sonagrammen und Spektrogrammen werden traditionell gerne z.B. die Diskrete Fourier Transformation (DFT), die Wavelet-Transformation oder quadratische Verfahren wie die Wigner-Ville-Transformation herangezogen. Viele Varianten sind hiervon bekannt. Doch alle scheitern, wenn es um präzise Zeit-/Frequenzanalyse im kritischen Bereich der bekannten Unschärferelation geht.
Diese Seite präsentiert eine neue Lösung, die die Zeit-Frequenzebene scharf darzustellen vermag und dabei ohne Kreuzterm-Störungen der quadratischer Verfahren auskommt. Eine variierende Zeit-/Frequenzauflösung wie bei der Wavelet-Transformation, die zudem bekanntlich nur die gleiche Abbildungsschärfe wie die DFT aufweist, gibt es ebenfalls nicht.
Die Software TFA ist das Zeit-Frequenzanalyse-Werkzeug für viele Forschungsgebiete. Etwa 15 Jahre Forschungs- und Entwicklungsarbeit wurden für die grundlegenden Technologien investiert, um eine meist wirklich unerreichte Analysequalität zu erhalten. Dieser Abschnitt gibt einige Beispiele aus verschiedenen Disziplinen.
Die folgenden Beispiele sind auch enthalten in: TFA-Applikationen.pdf [5.085 KB]
TFA eignet sich für jeden Fall von Zeit-Frequenzanalyse, Frequenzanalyse und Zeitsignalanalyse. Die Software kann ihre Vorteile aber besonders dann einbringen, wenn die Analysesituation durch die Unschärferelation betroffen ist. Letzteres ist sehr häufig der Fall, z.B. in der Nachrichtentechnik bei der Analyse von Kommunikationssignalen. Dann ist TFA für ein wirtschaftliches zielorientiertes Arbeiten oft absolut erforderlich.
Im Folgenden seien einige Analysebeispiele aus völlig unterschiedlichen Wissenschaftsbereichen vorgestellt und teilweise mit anderen dort verwendeten Analysewerkzeugen verglichen. Die Beispiele entstammen der
- 1. Nachrichtentechnik: Schmal- und breitbandige Funksignale
- 2. Sprachverarbeitung: Sprache
- 3. Geowissenschaften: Insolationsforschung, El-Nino–Phänomen, CO2-Konzentration, Sonnenfleckenanzahl
Es ist klar, dass sich die Liste beliebig fortsetzen ließe.
1. Nachrichtentechnik
In der Nachrichtentechnik, genauer: in der Funktechnik, möchte man einerseits einen Einblick über die Belegung eines Hochfrequenz (HF) –Bereichs erhalten und andererseits auch sofort die Art der vorhandenen Funksignale inkl. ihrer Signaleigenschaften einfach ablesen können.
1.1 Nachrichtentechnik: Schmalbandiges Funksignal
Dieses Beispiel zeigt ein FSK-ARQ-Signal, das bedeutet: Eine Funkstation sendet eine kurze Nachricht in der Modulationsart FSK, der Empfänger quittiert die Nachricht mit einem kurzen FSK-Block. Sendung und Quittung wechseln sich ab, bis die komplette Datenübertragung abgeschlossen ist.
1.1.1 Gewöhnliches FFT-Spektrogramm:
Die herkömmliche FFT-Spektrogrammanalyse ergibt folgende Abbildung:
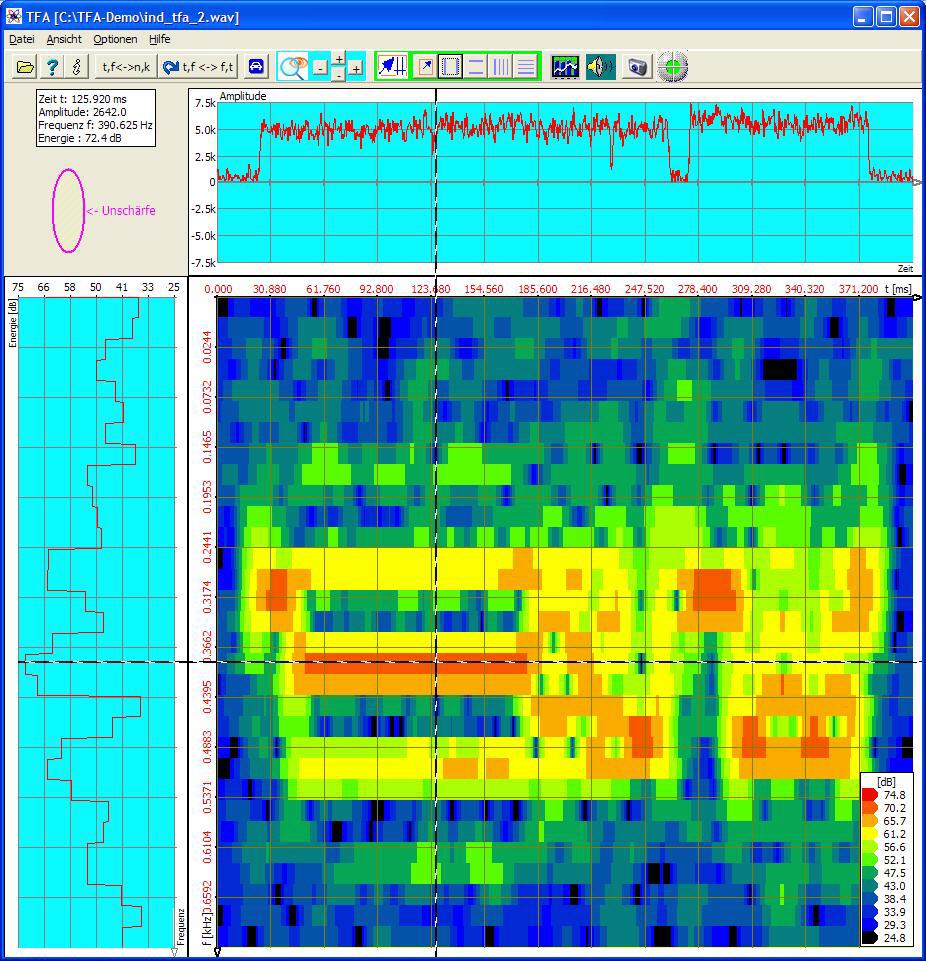
Die FFT-Länge von 256 liefert hier einen guten Kompromiss zwischen Zeit- und Frequenzunschärfe, siehe Unschärfe-Ellipse links oben. Doch weder Zeit- noch Frequenzverhalten lässt sich dem Spektrogramm entnehmen.
1.1.2 Genaue DXP-Spektrogrammanalyse:
Die DXP-Analyse gestattet die getrennte Einstellung von Zeit- und Frequenzauflösung, vgl. folgende Abbildung desselben Signals:
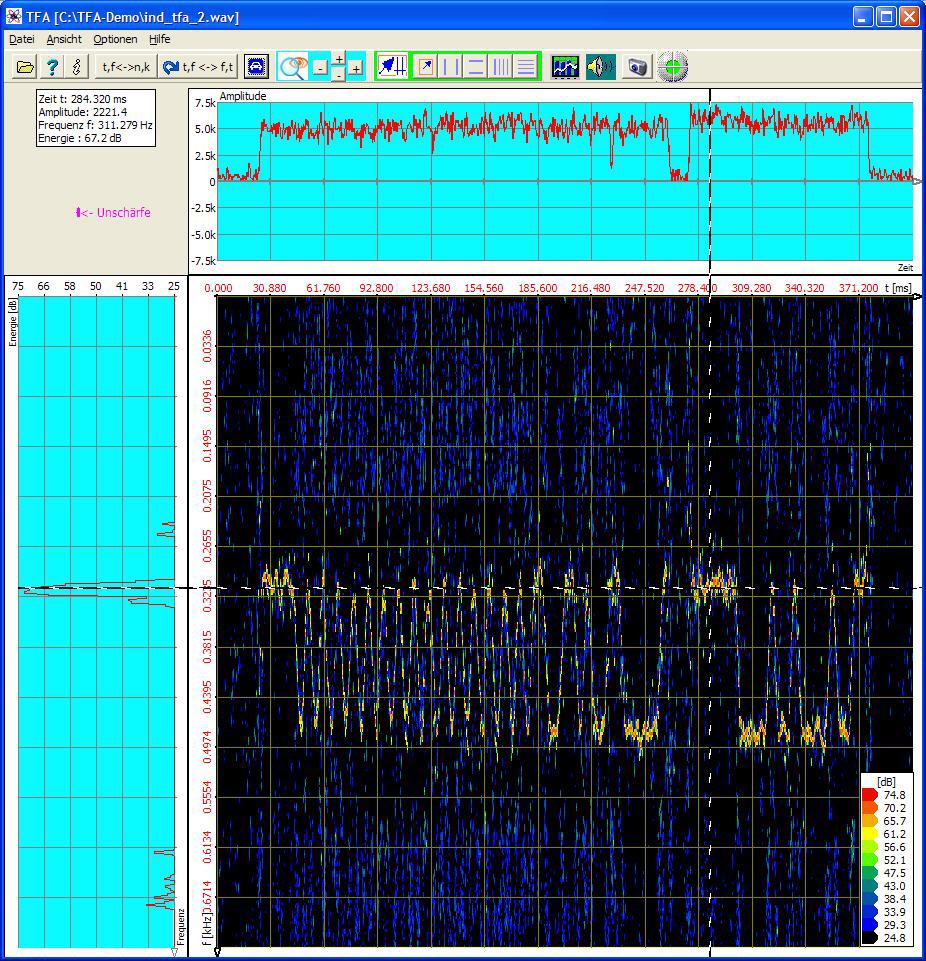
Man erkennt das FSK-ARQ-Signal bereits recht deutlich, weil die Fläche der Unschärfe-Ellipse um den Faktor 2048/32 = 64 geringer ist.
Ein beliebiger Zoom in den rechten Spektrogrammbereich ergibt folgende Darstellung. Mit Hilfe der vertikalen und horizontalen Marker lässt sich das Signal auch gleich schnell vermessen:
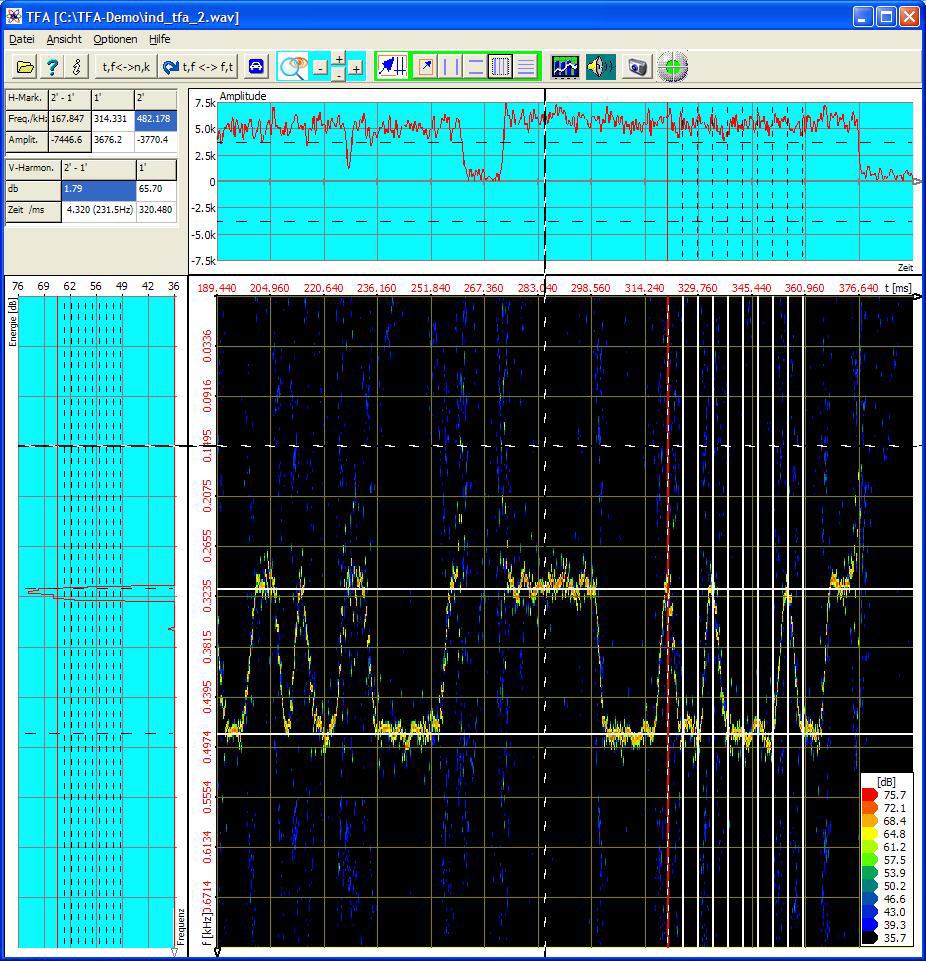
Sofort lassen sich in den Marker-Wertetabellen die wichtigen FSK-Merkmale, z.B. die Baudrate SG= 230 Bd, ablesen.
Man beachte, wie gut das DXP-Spektrogramm auch die Signalpause zwischen den beiden Sendungen wiedergibt.
1.2 Nachrichtentech.: Breitbandig. HF-Funkszenario
Dieses Beispiel zeigt einen Einblick in ein relativ breites Frequenzband, in dem mehrere Funkteilnehmer kommunizieren.
1.2.1 Gewöhnliche FFT-Spektrogrammanalyse:
Die herkömmliche FFT-Spektrogrammanalyse ergibt folgende Abbildung:
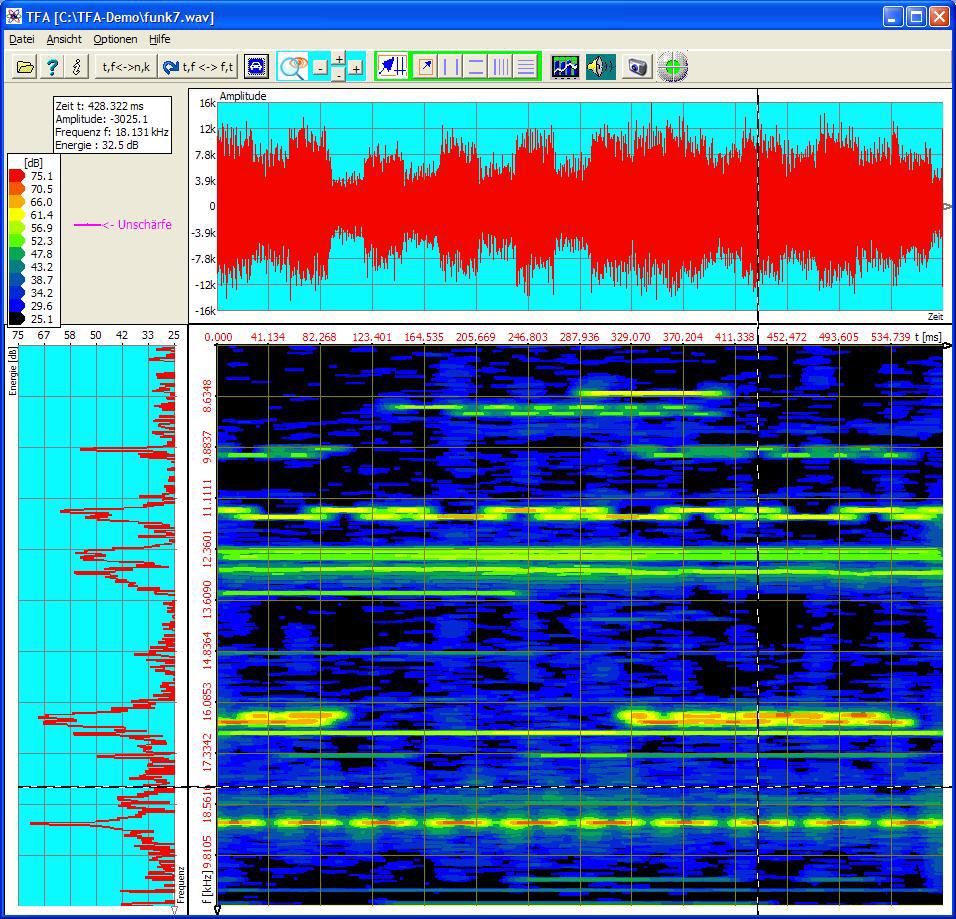
Um die einzelnen Sender im Frequenzbereich trennen zu können, bedarf es einer höheren FFT-Länge von hier z.B. 2048. Die magenta-farbene Unschärfeanzeige oben-links zeigt daher eine in Bezug auf die vorliegenden Signale hohe Zeitunschärfe von etwa 50 ms an. Dies verschmiert die Darstellung des Zeitverhaltens der unterschiedlichen Funkteilnehmer.
1.2.2. Genaue DXP-Spektrogrammanalyse:
Die DXP-Analyse gestattet die getrennte Einstellung von Zeit- und Frequenzauflösung, vgl. folgende Abbildung desselben Signals:
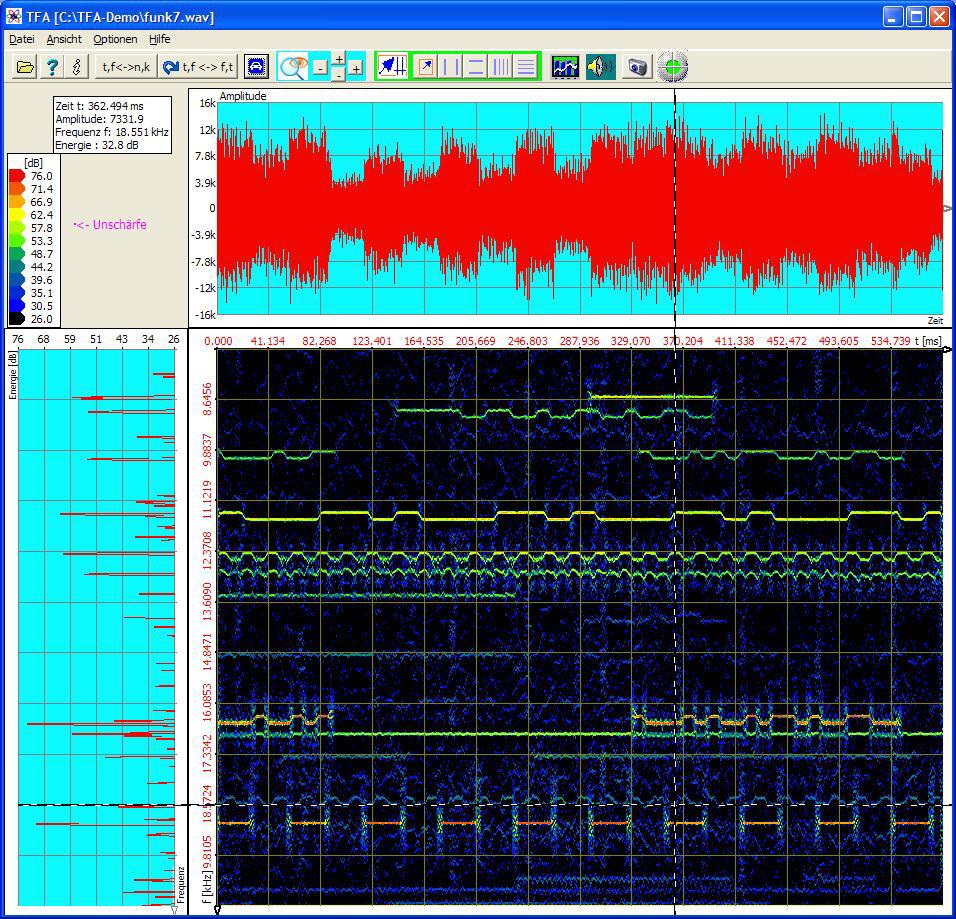
Die einzelnen Kommunikationssignale sind nun wesentlich präziser zu sehen und natürlich auch zu vermessen, weil die Abbildungsschärfe um den Faktor 4096/256 = 16 geringer ist.
2. Sprachverarbeitung: Sprache
Die elektronische Verarbeitung von gesprochener Sprache ist es und wird noch auf lange Zeit ein viel beachtetes Forschungsgebiet bleiben. Zur Analyse von Sprachsignalen ist die Zeit-Frequenzdarstellung eines der Hauptwerkzeuge. Dieses Beispiel zeigt Spektrogramme eines beliebigen Sprachsignals im stimmhaften Frequenzbereich von 0 … 1.5 kHz. Dabei kommt wieder neben der herkömmlichen FFT die spezielle DXP-Berechnung zum Einsatz.
2.1 Gewöhnliche FFT-Spektrogrammanalyse des Sprachsignals:
Die herkömmliche FFT-Spektrogrammanalyse ergibt folgende Abbildung:
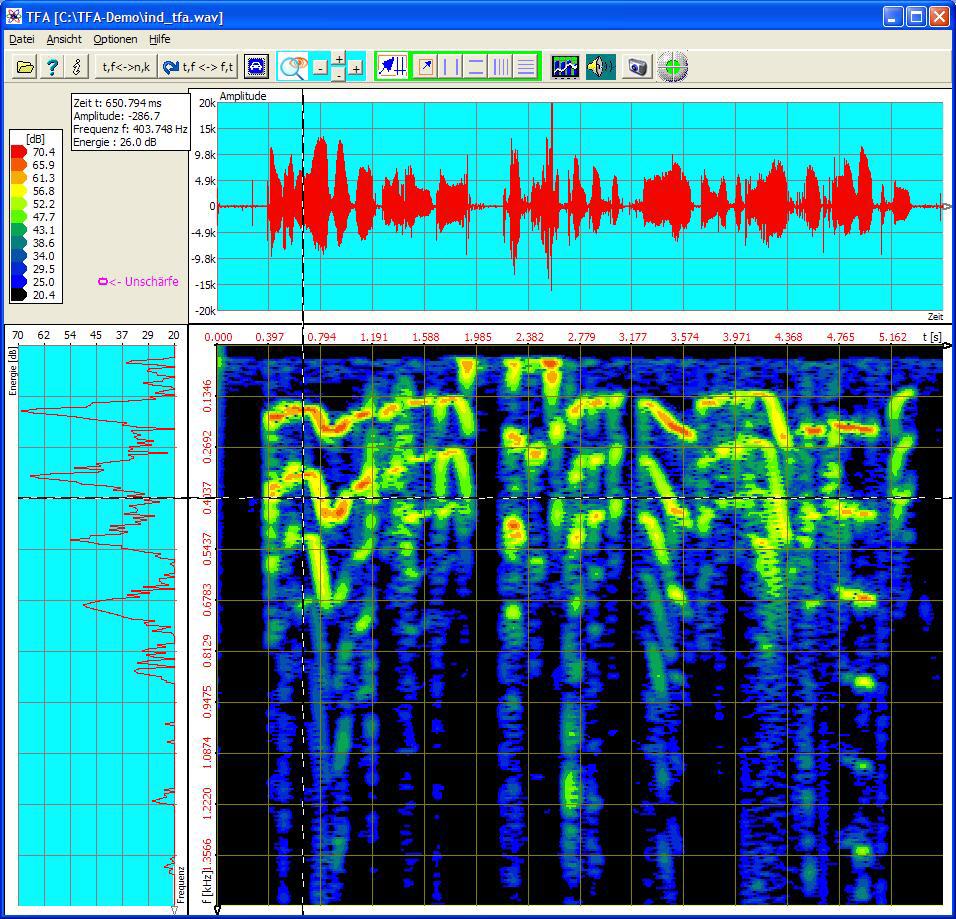
Die FFT-Länge von 2048 liefert einen guten Kompromiss zwischen Zeit- und Frequenzunschärfe, siehe Unschärfe-Ellipse links oben.
Theoretisch sollten aber nur diskrete Linien zu erkennen sein, denn der menschliche Stimmapparat generiert den stimmhaften Laut zeitvariant als konkreten Grundton mit zugehörigen Oberwellen.
Auch diese lässt sich mit TFA darstellen, siehe nächster Abschnitt.
2.2. Genaue DXP-Spektrogrammanalyse des Sprachsignals:
Die DXP-Analyse gestattet die getrennte Einstellung von Zeit- und Frequenzauflösung, vgl. folgende Abbildung desselben Signals:
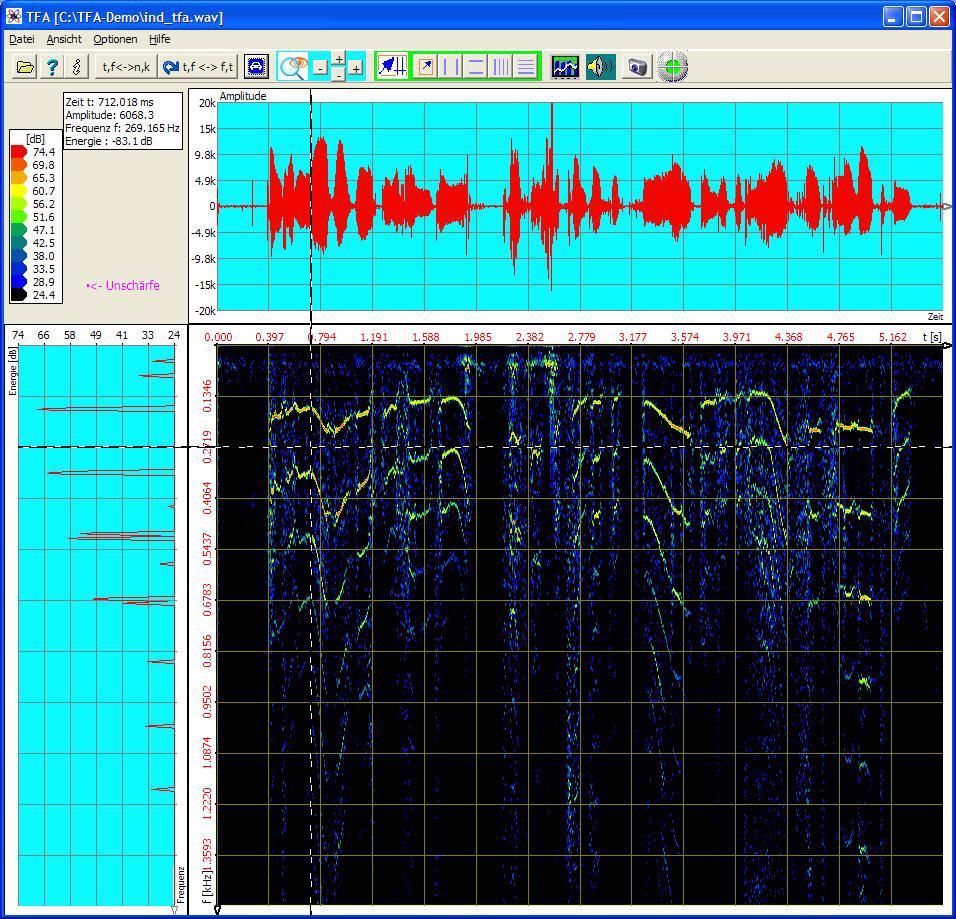
Die einzelnen Stimmkomponenten sind nun wesentlich präziser zu sehen und natürlich auch zu vermessen, weil die Abbildungsschärfe um den Faktor 4096/256 = 16 geringer ist.
3. Geowissenschaften
Bei der Erforschung unseres Planeten und des Universums ist die Zeit-Frequenzanalyse ebenso ein unverzichtbares Werkzeug. Allerdings laufen viele zyklische Vorgänge sehr langsam und in Zeiträumen ab, deren Frequenz nicht mehr anschaulich in Hertz [Hz] angegeben werden kann. Viele natürliche Vorgänge haben darüber hinaus mit der Rotation der Erde um die Sonne zu tun, weswegen an die Stelle der Frequenzangabe in [Hz] die Messung der Periodendauer in Jahren [yr], tausend Jahren [kyr] oder sogar Jahrmillionen [Myr] tritt.
Beispiele solcher Forschung sind:
- Insolationsforschung, Sonnenbestrahlung der Erde zur Beurteilung der Erderwärmung.
- El-Nino–Phänomen, Auftreten von veränderten Strömungen im ozeanografisch-meterologischem System des Pazifiks, wodurch der Humboldtstrom vor der Küste Südamerikas abreißt.
- CO2-Konzentration, Untersuchung des Treibhauseffekts.
- Sonnenfleckenzahl, Untersuchung der Sonnenaktivität.
3.1 Geophysik: Insolationsforschung
Die Insolation bezeichnet die Sonnenbestrahlung der Erde in Watt pro Quadratmeter [W/qm]. Klimaforscher berechnen Zeitreihen der Insolation durch Entnahme und Analyse von Bohrkernen, welche im Eis der Arktis bei etwa 65 Grad nördlicher Breite gewonnen werden. Die Insolation ist zeitlich variant, weil sich die Erdumlaufbahn im Laufe der Jahrmillionen ändert.
Weiteres hierzu: Insolation
Ein geeignetes Analyseverfahren sollte möglichst alle der in Insolation genannten Periodizitäten nachweisen können, also Periodizitäten von etwa
- 413.000 Jahren (413 kyr)
- 100.000 Jahren (100 kyr)
- 41.000 Jahren (41 kyr)
- 23.000 Jahren (23 kyr) und
- 19.000 Jahren (19 kyr).
Darüber muss eine eventuelle Variation der Periodizitäten nicht nur feststellbar, sondern auch genau vermessbar sein.
3.1.1 Gewöhnliche FFT-Spektrogrammanalyse der Insolation
Die herkömmliche FFT-Spektrogrammanalyse ergibt folgende Abbildung:
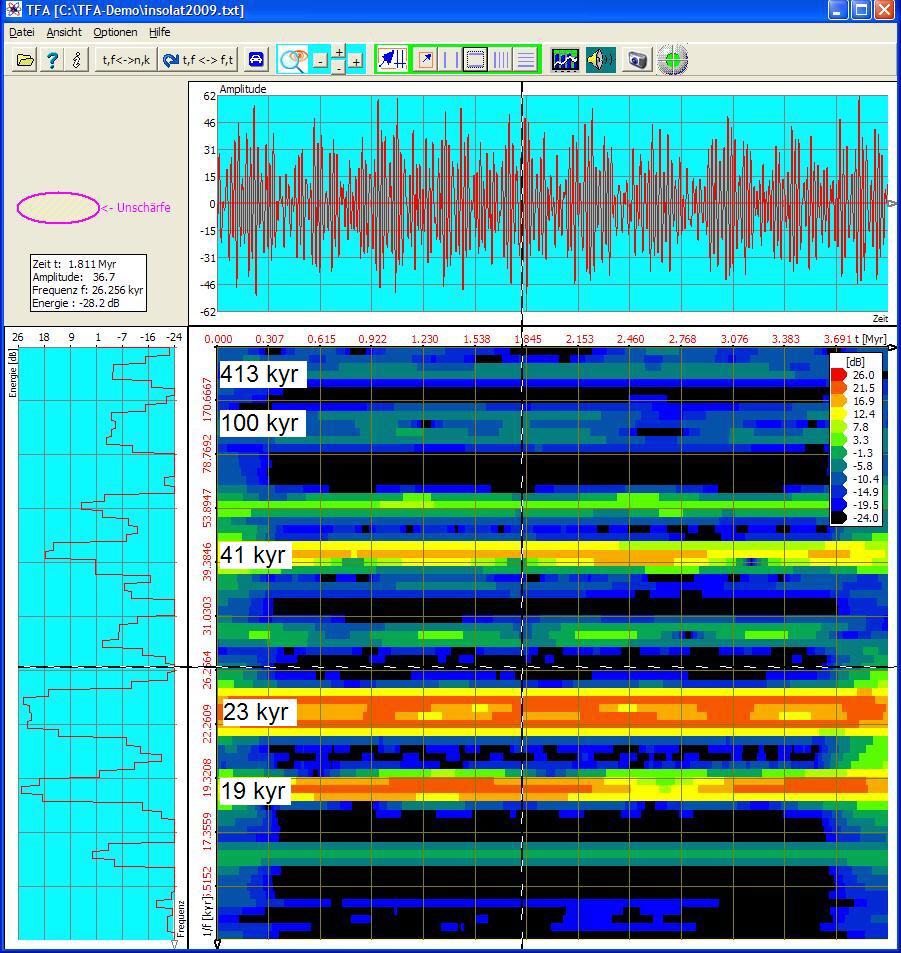
Die FFT-Länge von 1024 liefert einen guten Kompromiss zwischen Zeit- und Frequenzunschärfe, siehe Unschärfe-Ellipse links oben.
Die erwarteten Periodizitäten sind durchaus deutlich zu sehen. Man sieht aber auch, dass z.B. die Schwingung mit der Periode 23 kyr noch weitere Signaldetails enthalten muss. Diese lassen sich mit der FFT unabhängig von der gewählten Transformationslänge nicht erfassen.
3.1.2 Genaue DXP-Spektrogrammanalyse der Insolation
Die DXP-Analyse gestattet die getrennte Einstellung von Zeit- und Frequenzauflösung, vgl. folgende Abbildung desselben Signals bei zusätzlicher Vergrößerung des TFA-Fensters, um mehr Grafikpixel zu belegen:
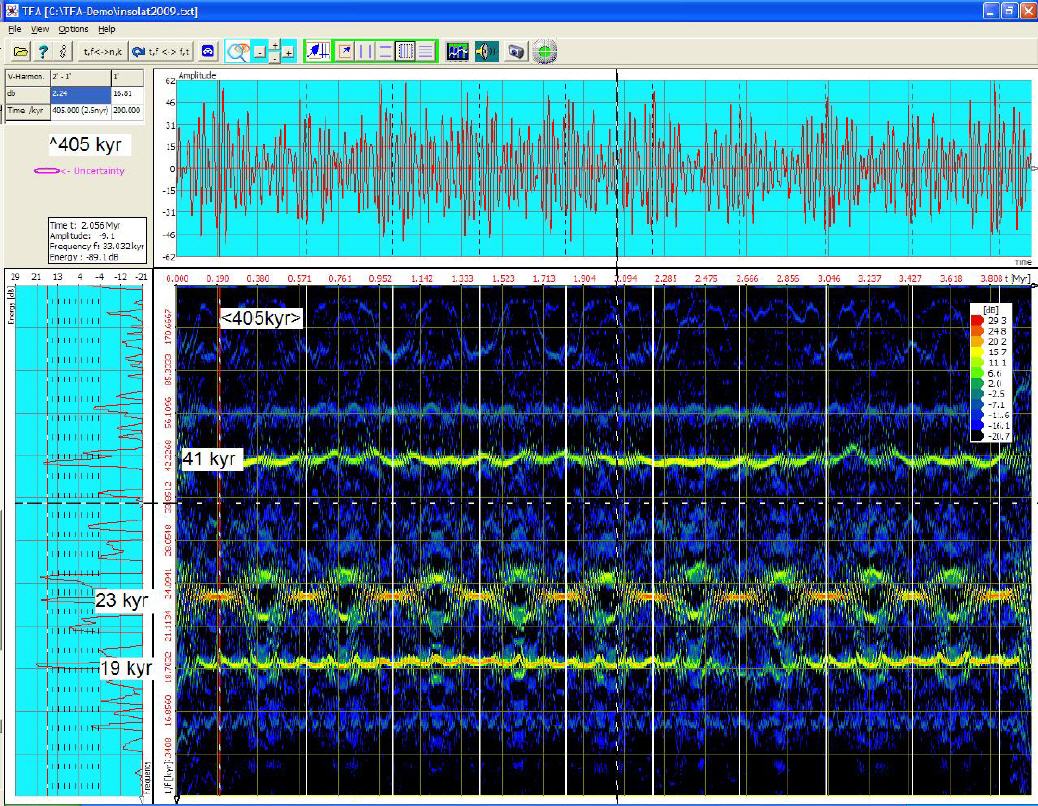
Das DXP-Spektrogramm gestattet einen Einblick z.B. in die Beschaffenheit der 23-kyr-Komponente. Man erkennt, dass
- die angenommene niederfrequente 413-kyr-Komponente mit dem Harmonic-Marker tatsächlich genauer zu 405 kyr bestimmt werden kann und
- diese 405-kyr-Komponente in Wirklichkeit eine Modulation der 23-kyr-Komponente ist, und nicht eigenständig. Deswegen erscheint die 413-kyr-Komponente weniger ausgeprägt an der entsprechenden Position der Frequenzachse, sondern als Modulation der 23-kyr-Komponente.
Den Aspekt der Modulation findet man auch in der Zeitdarstellung oberhalb des Spektrogramms bestätigt. Allerdings ist dort natürlich nicht zu sehen, dass die 23-kyr-Komponenten die modulierte ist.
3.2 Geophysik: El-Nino-Phänomen
Das El-Nino-Phänomen bezeichnet das Auftreten von veränderten Strömungen im ozeanografisch-meterologischem System des Pazifiks, wodurch der Humboldtstrom vor der Küste Südamerikas abreißt. Es ist bis heute noch nicht vollständig erforscht. Alle 3-8 Jahre kommt es zu einer starken Erwärmung des Meerwassers.
Auch bei der Analyse dieser Temperaturdaten handelt es sich um eine Zeit-Frequenzanalyse-Aufgabe.
Häufig wird die sog. WAVELET-Transformation verwendet, weil sie eine frequenzabhängige Unschärfeverteilung in der Zeit-Frequenzebene aufweist:
- Tiefe Frequenzkomponenten lassen sich in ihrer Frequenz genau messen, aber sie sind zeitlich schlecht lokalisiert, was unterstellt, dass die tiefe Frequenzkomponente für einen relativ langen Zeitraum existiert.
- Hohe Frequenzkomponenten sind zeitlich mit wachsender Frequenz genauer zu lokalisieren, dafür nimmt die Präzision der Frequenzmessung ab, meist in Schritten von Zweierpotenzen.
Obwohl jeweils beide Punkte für allgemeine Analyseaufgaben eigentlich ein Ausschlusskriterium sein müssten, erfreut sich die WAVELET-Transformation einer großen Beliebtheit. Aus diesem Grund sollen die Analysen des El-Nino-Phänomens mit der WAVELET-Transformation und TFA-DXP einander gegenüber gestellt werden.
3.2.1 Gewöhnliche Wavelet-Analyse des El-Nino-Phänomens
Folgende Abbildung zeigt das Ergebnis einer Wavelet-Analyse des El-Nino-Phänomens:
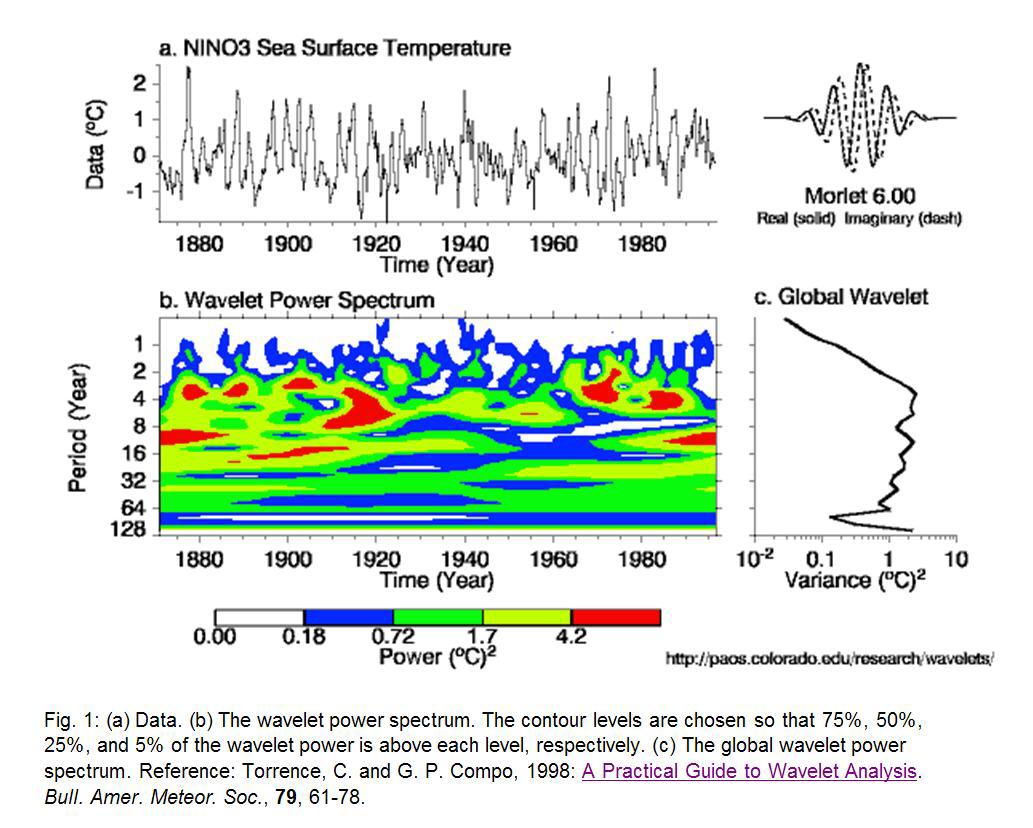
Der Grafik lässt sich entnehmen, dass sehr hohe Temperaturen mit überlagerten Perioden von ca. 3-20 Jahren auftreten. Leider sind rechts und links ebenfalls rote Bereiche zu sehen, obwohl die Temperaturmessung gerade hier relativ niedrige Werte aufweist.
3.2.2 Genaue DXP-Spektrogrammanalyse des El-Nino-Phänomens
Das DXP-Spektrogramm mit einem Zeitfenster von ca. 3.5 Jahren (14 Messwerte) zeigt die nächste Abbildung.
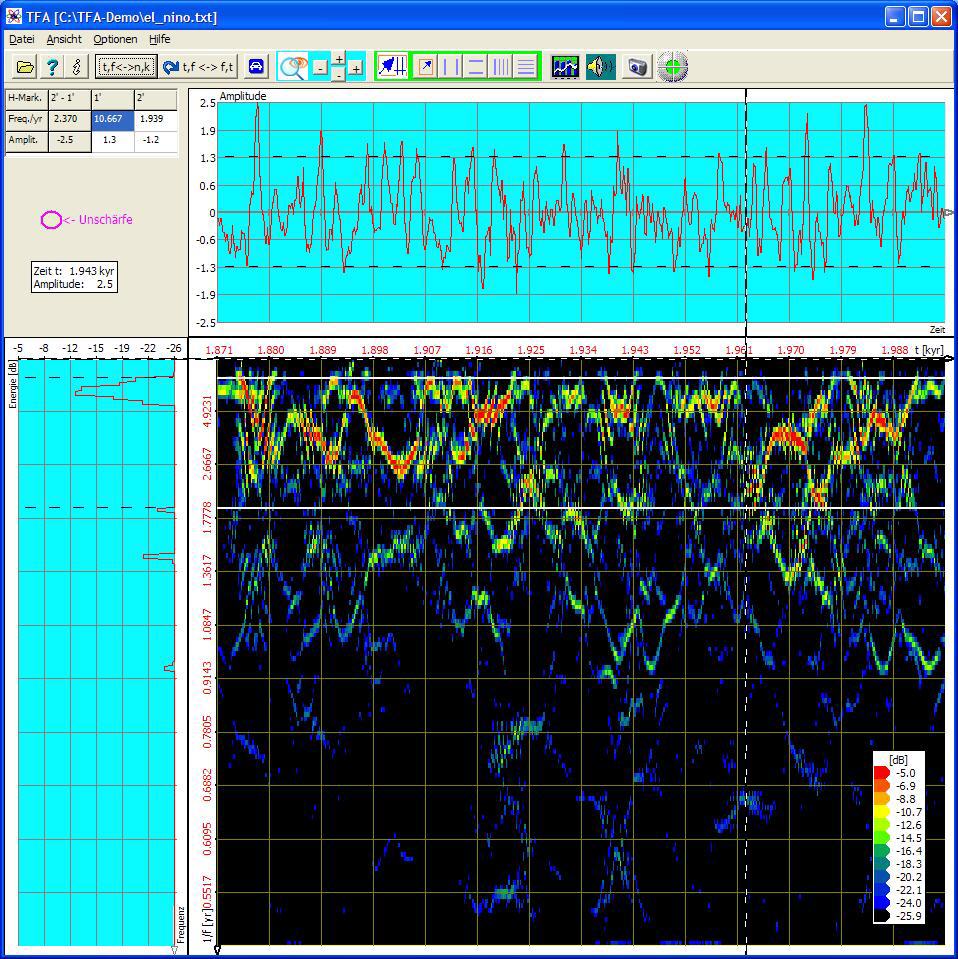
Man sieht in guter Übereinstimmung mit der Theorie, dass
- die Periode des El-Nino-Phänomens tatsächlich im Bereich von 3-8 Jahren liegt. Mit den horizontalen Markern findet man, dass sie vereinzelt auch mal 1,939 – 10,667 Jahre sein kann.
- Im Wesentlichen hat man es aber mit nur einer einzigen variierenden Komponente zu tun.
- Das Spektrogramm korrespondiert auch an den Rändern mit der Temperaturmessreihe.
3.3 Geophysik: CO2-Konzentration
Die Bedeutung der Konzentration des Treibhausgases CO2 in der Erdatmosphäre muss heute nicht mehr erläutert werden. Auch für diese Analyse wird gerne die Wavelet-Transformation verwendet, obwohl sie den Sachverhalt nur teilweise wiedergeben kann.
Eine CO2-Analyse sollte folgendes zeigen können:
- Es ist allgemein bekannt, dass die mittlere CO2-Konzentration in den letzten Jahrzehnten zugenommen hat und weiter ansteigt. Es gibt also einen Trend.
- Die CO2-Konzentration schwankt im Laufe des Jahres um diesen Trend.
- Der Jahreszyklus ist nicht sinusförmig.
Im Folgenden ist die Wavelet-Analyse der TFA-DXP-Analyse gegenübergestellt.
3.3.1 Gewöhnliche Wavelet-Analyse der CO2-Konzentration
Folgende Abbildung zeigt das Ergebnis einer Wavelet-Analyse der CO2-Analyse:

Deutlich ist die Schwankung der CO2-Konzentration mit der Jahresperiode zu sehen.
Aber:
- Da die Schwankung nicht sinusförmig ist, sollte außerdem mindestens eine Oberwelle mit Bruchteilen der Jahresperiode angezeigt werden. Eine Oberwelle ist nicht zu erkennen.
- Der ansteigende Trend des Kurvenverlaufs ist ein sehr niederfrequentes Kurvendetail. Die Wavelet-Transformation besitzt im niederfrequenten Bereich eine sehr schlechte zeitliche Lokalisierung und kann die Zeitabhängigkeit der mittleren Konzentration nicht wiedergeben.
- Die U-förmige Energieverteilung entspricht natürlich nicht der Realität und zeigt lediglich die frequenzabhängige Unschärfe der Wavelet-Transformation.
Die Wavelet-Transformation kann zur Analyse der CO2-Konzentration nur bedingt eingesetzt werden.
3.3.2. Genaue DXP-Spektrogrammanalyse der CO2-Konzentration
TFA besitzt eine Option „DC-Offset-Korrektur“ zur Beseitigung der Grundkonzentration, also des Kurvensockels. In der Praxis ist man natürlich ebenso an dieser DC-Komponente interessiert, doch im Hinblick auf die Analyse handelt es sich um eine triviale Größe. Durch die Subtraktion der Grundkonzentration tritt der Trend deutlicher hervor.
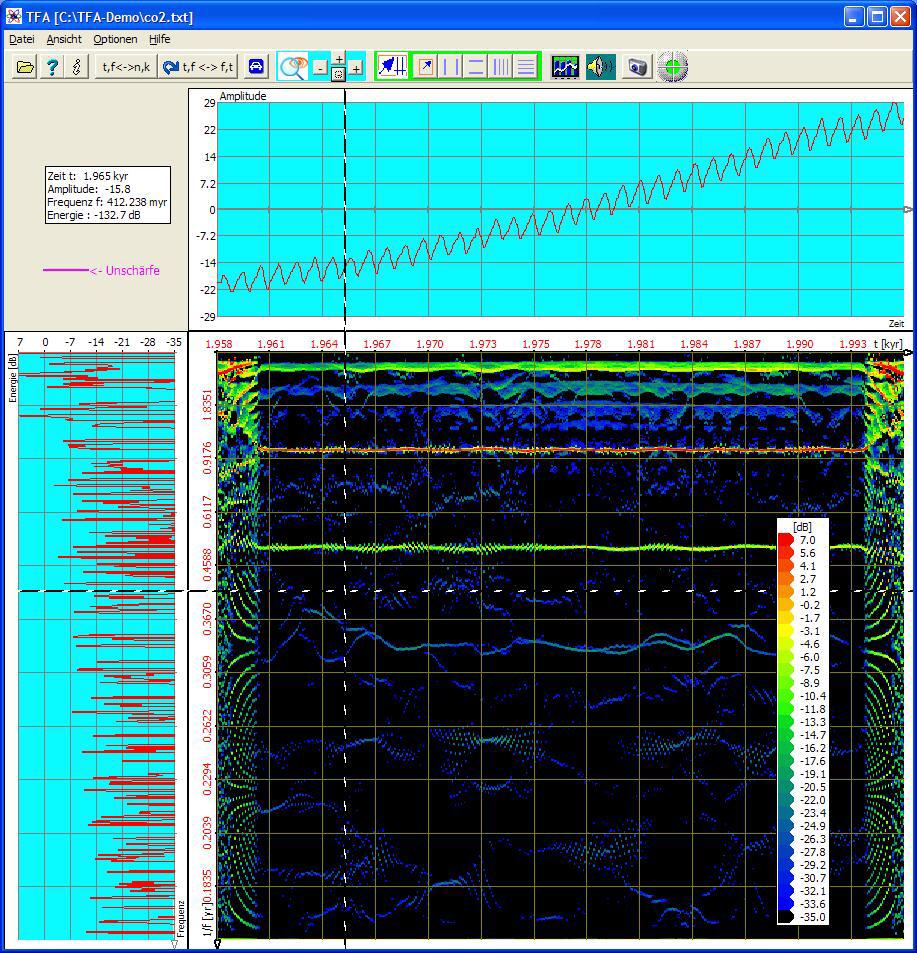
Man sieht sehr schön
- die Jahresschwankung mit der Periode 1 Jahr, die wegen der hohen Frequenzauflösung von 2048 Linien sehr genau messbar ist,
- eine Oberwellenschwingungskomponente der Periode 0.5 Jahre,
- den Trend nach einem Zoom in den niederen Frequenzbereich, vgl. nächste Abbildung.
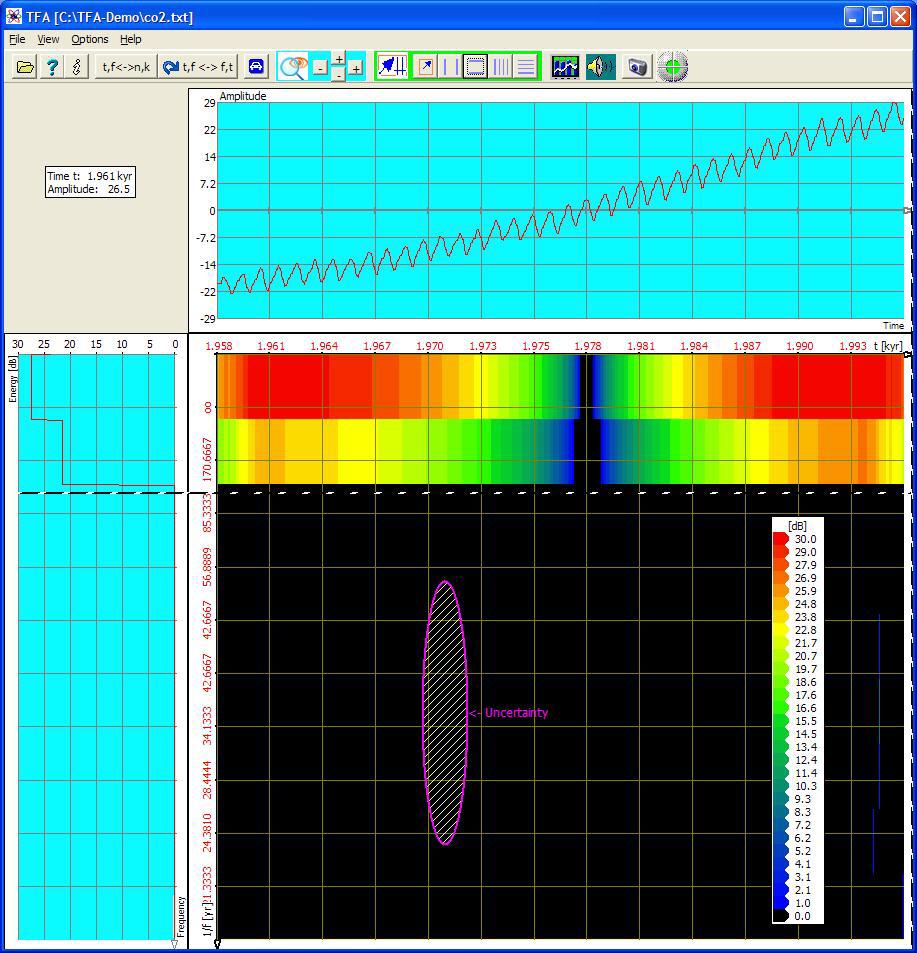
Durch die DC-Offsetkorrektur verläuft die Kurve durch die Zeitachse. An dieser Stelle ist die Trendenergie Null, was auch das Spektrogramm zeigt. Jenseits des Nulldurchgangs nimmt die Trendenergie zu. Die präzise Trendanalyse ist möglich, weil die Zeit-Frequenzunschärfe im Gegensatz zur Wavelet-Transformation auch im Niederfrequenzbereich gering ist, vgl. Unschärfeellipse.
3.4 Geophysik: Sonnenflecken
Sonnenflecken sind dunkle Punkte auf der Sonnenoberfläche, die eine dort geringere Temperatur anzeigen. Die Sonnenfleckenanzahl hängt mit der Sonnenaktivität zusammen und variiert mit einer schwankenden Periode von etwa 11 Jahren (Sonnenfleckenzyklus). Die Periodenschwankungen lassen sich mit Hilfe der Zeit-Frequenzanalyse feststellen.
Im Folgenden ist wieder die Wavelet-Analyse der TFA-DXP-Analyse gegenübergestellt.
3.4.1 Gewöhnliche Wavelet-Analyse der Sonnenfleckenzahl
Folgende Abbildung zeigt das Ergebnis einer Wavelet-Analyse der Sonnenfleckenzahl:
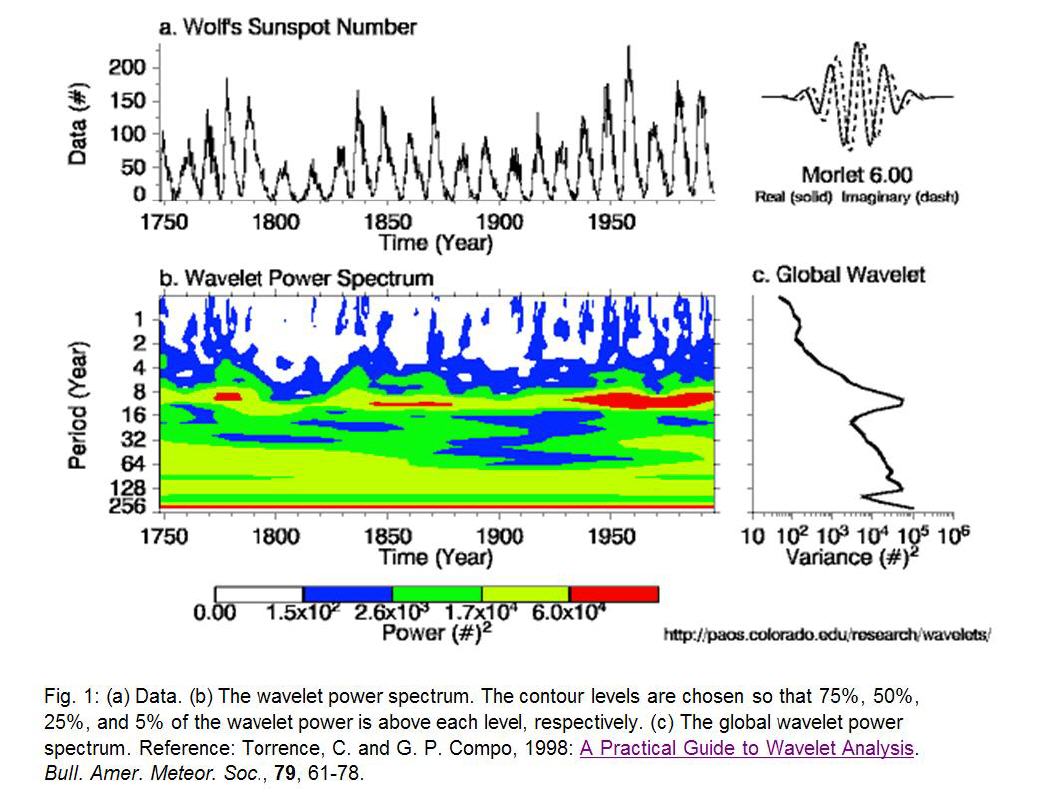
Erwartungsgemäß ist eine charakteristische Ausprägung im Periodenintervall 8-16 Jahre zu erkennen. Obwohl das Zeitsignal teilweise eine gut ausgeprägte Periodizität aufweist, ist die Wavelet-Verteilung meist relativ unscharf.
3.4.2 Genaue DXP-Spektrogrammanalyse der Sonnenfleckenzahl
Mit TFA lässt sich die Periode des Sonnenfleckenzyklus zumindest zu den Zeitpunkten deutlicher Periodizität mit der Genauigkeit von etwa 0.1 Jahr genau messen. Mit dem Mauszeiger ist hierzu einfach jeder gewünschte Punkt in den Grafiken anzufahren.
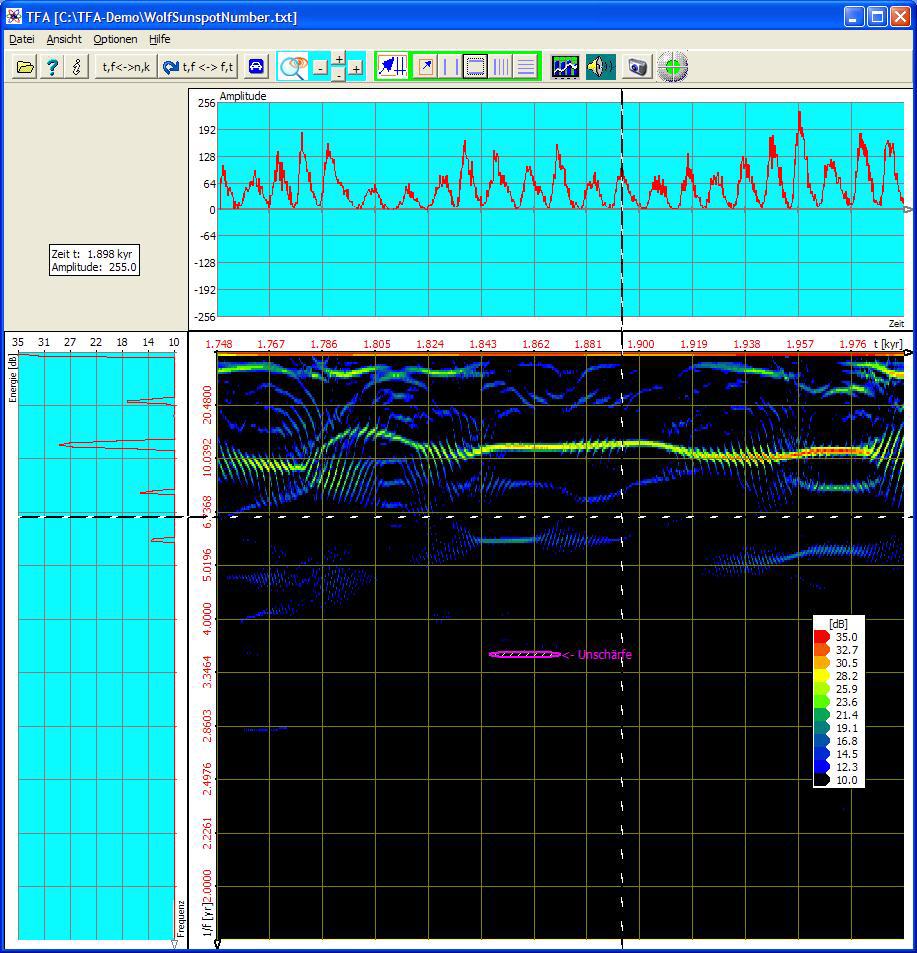
Bei einer Erhöhung der FFT-Länge auf 4096 verringert sich die Unschärfefläche in vertikaler Richtung, während sich die zeitliche Unschärfe nicht ändert.
Diese Beispiele sind auch enthalten in: TFA-Applikationen.pdf [5.085 KB]