DXP-Spektralanalyse

DXP - Eine neue Technologie ...

... am Beispiel der Spektralanalyse

Seit Werner Heisenberg im Jahre 1927 seine berühmte Unschärferelation der Quantenmechanik formulierte, hat auch ihre Analogie in der Nachrichtentechnik eine besondere Aufmerksamkeit erfahren. Die strenge Konsequenz lautet hier, dass sich nicht gleichzeitig Frequenz und Zeitpunkt eines Schwingungspakets genau messen lassen – bis heute.

Die Unschärferelation der Nachrichtentechnik

Gemäß der nachrichtentechnischen Unschärferelation bedingen höhere Anforderungen an die Frequenzmessgenauigkeit eine bestimmte Mindestlänge des in die Rechnung eingehenden Messzeitintervalls.
Messtechniker kennen das von der Wahl der Torzeit bei Frequenzzählern oder der Fourier-Transformationslänge bei herkömmlichen FFT-Spektralanalysatoren.
Leider kann man in der Praxis nicht immer unterstellen, dass das zu vermessende Signal für jede gewünschte Dauer zur Verfügung steht.
Und Kurzzeitmessungen haftet umgekehrt der Makel einer geringeren Frequenzauflösung an.

Herkömmliche Lösungen

zur Kurzzeit-/Frequenzanalyse

• unterliegen daher unabhängig vom eingesetzten Rechenverfahren exakt den o.a. Beschränkungen.
• Oder gravierender noch: Es zeigen sich Phantomstörungen aufgrund sog. Kreuzterme, die in anspruchsvoller Messtechnik nicht akzeptabel sind.

Der Ausweg des Dilemmas heißt DXP!

(Unser DXP hat nichts mit dem von der Firma Sony entwickelten "Digital Extended Processor" zu tun, einem Prozessor, der nicht nur digitale Signale verarbeiten kann.)

Dieser Abschnitt gibt einen kurzen Überblick über DXP und Einsatzgebiete.
Viele weitere Beispiele aus mehreren Wissenschaftsbereichen wie z.B. der
Geophysik mit z.B. den Themen Insolation, El-Nino-Phänomen, Co2-Konzentration
gibt es hier: TFA in der Forschung
oder als PDF-Datei TFA-Applikationen.pdf [5.085 KB] .

Beispiel aus der Nachrichtentechnik

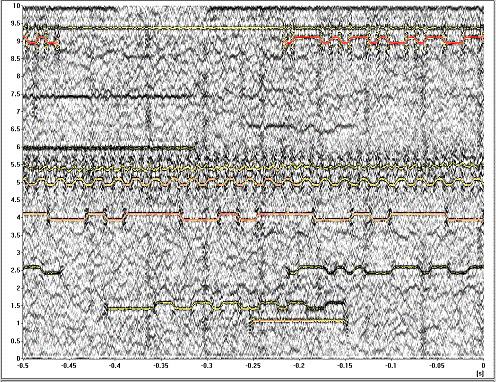
Folgende Darstellungen zeigen im praktischen Vergleich die Zeit-/Frequenzanalyse (Spektrogramm) eines HF-Bandes - oben auf Basis der meist verwendeten Fast-Fourier-Transformation (FFT) und darunter mit DXP-Berechnung.

In y-Richtung ist die Frequenzbelegung aufgetragen, in x-Richtung der zeitliche Verlauf.

Die Energie ist farblich kodiert, wobei hohe Energien rot und der Rauschbereich grau erscheint.

Der Schärfegewinn durch DXP sowohl in Frequenz- als auch Zeitrichtung ist deutlich zu erkennen. Er ist einstellbar und beträgt hier "nur" Faktor 8!

Folgende Darstellung zeigt das DXP-Spektrogramm als Voraussetzung erfolgreicher und exakter Signalvermessung:

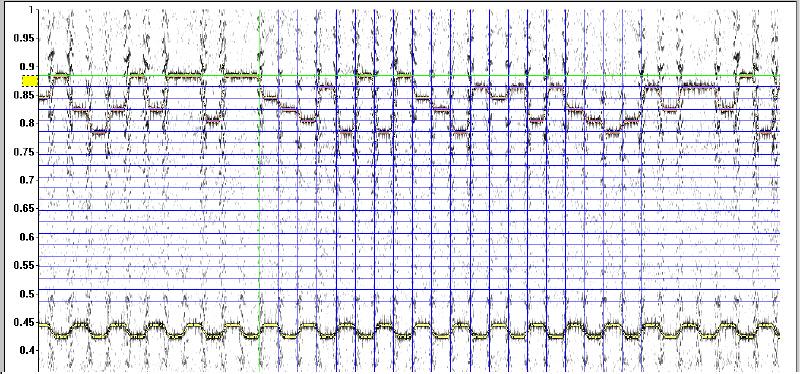
Beispiel aus der Sprachanalyse

Eine Möglichkeit der Sprachanalyse ist die Vermessung der Formanten, des Spektrums der menschlichen Stimme. Die Ausprägung der Formanten in Zeit- und besonders Frequenzbereich bestimmt direkt die Klangfarbe der Stimme und ist somit ein maßgebliches Kriterium bei der Sprechererkennung.

Häufig wird auch für diesen Zweck die bekannte Fast-Fourier-Transformation FFT eingesetzt. Doch ihre mangelhafte Präzision bei der Zeit-/Frequenzanalyse beschränkt die Aussagekraft der Ergebnisse.

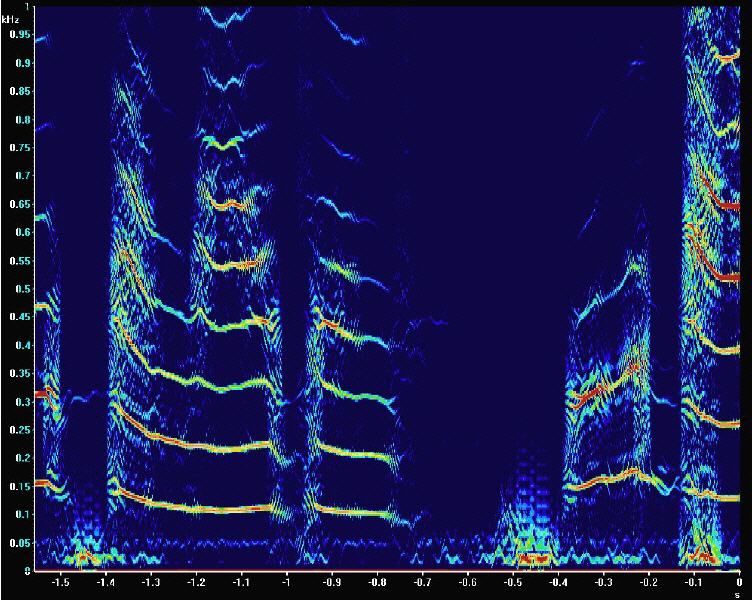
Folgende Bilder zeigen einen kurzen Ausschnitt eines Sprachsignals in der Frequenz-/Zeitebene bei Vermessung zunächst mit Hilfe der FFT, darunter mit DXP-Unterstützung:

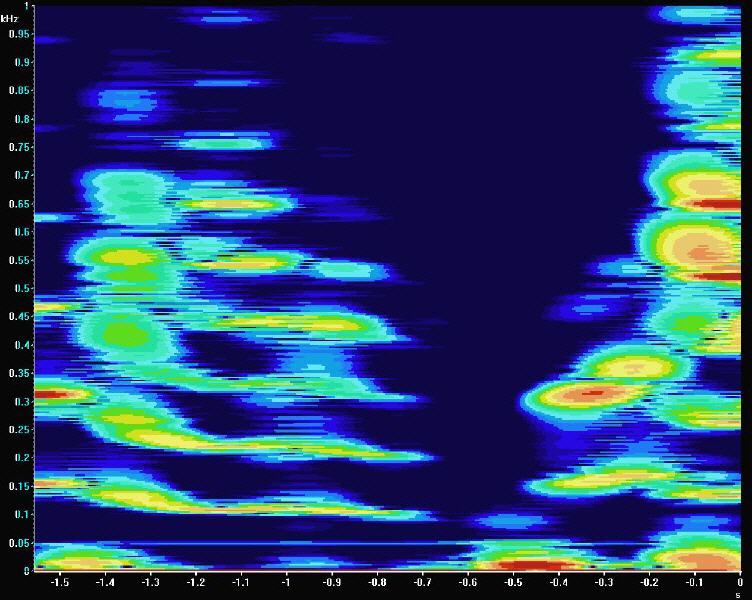
Mit DXP-Rechnung zeigt sich abermals der bedeutende Schärfegewinn. Sollten die Spektrogramme etwa zur Sprecherklassifizierung verwendet werden, führt der Einsatz von DXP zu einer erheblichen Steigerung der Klassifikationsqualität.

Wie arbeitet DXP?

DXP ist ein Softwarealgorithmus, der die Charakteristika selbst eines Kurzzeitsignals relativ genau erfassen kann. Mit diesen Erkenntnissen gelingt eine akkurate Langzeitprädiktion (Expandierung), welche anschließend einer herkömmlichen Spektralanalyse mit Fast Fourier Transformation FFT entsprechend höherer Transformationslänge unterzogen werden kann.

Einige Anwendungen: Technische Daten

• Spektralanalyse: Hier lassen sich praktisch unvermeidbare Unschärfen in der Zeit-/Frequenzebene um typisch Faktor 8 bis 32 verringern. Dabei funktioniert DXP auch mit Frequenzgemischen, wobei keine Kreuzterm-Störungen auftreten, wie sie von anderen Lösungen bekannt sind!
• Signalkompression: Durch die phasenrichtige Prädiktion ist DXP zur verlustlosen Datenreduktion einsetzbar. Der Kompressionseffekt beruht darauf, dass nur noch geringe Prädiktionsfehler (signalabhängig typ. 20 dB unter Aussteuerung) die gesamte Information enthalten.
• Digitale Filter im Zeit- und Frequenzbereich: Auch diese Elementarfunktionen sind von der Unschärferelation determiniert. Die Argumentation für DXP gilt hier daher in analoger Weise.
• Extrapolation von Daten.

Wie dargelegt und sofort nachvollziehbar ist das Einsatzgebiet für DXP schier unbegrenzt. Der jeweils erzielte Qualitätsgewinn ist grundsätzlich und objektiv nachzuweisen.

Dieser Abschnitt gab einen kurzen Überblick über DXP und Einsatzgebiete.
Viele weitere Beispiele aus mehreren Wissenschaftsbereichen wie z.B. der
Geophysik mit z.B. den Themen Insolation, El-Nino-Phänomen, Co2-Konzentration
gibt es hier: TFA in der Forschung
oder als PDF-Datei TFA-Applikationen.pdf [5.085 KB] ...

.... sowie Ausgabe 1504 der Zeitschrift "Elektronik" des Weka Verlags mit DXP-Anwendungen, etwas Mathematik und Son@Pro (Sonagrammprozessor Son@Pro) :

http://www.elektroniknet.de/

Eine sehr leistungsfähige und vielseitige Software, die ebenfalls DXP enthält, ist TFA-Zeit-Frequenzanalyse.